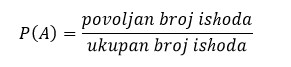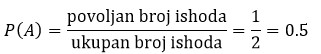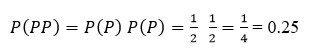Osnovni pojmovi i formule u verovatnoći

U realnosti se susrećemo sa neizvesnošću po mnogim pitanjima i samim tim preuzimamo na sebe odgovarajući rizik donošenja odluka, u lično ime ili za kompaniju za koju radimo. Zato je od koristi odgovoriti na pitanje: Koja je šansa uspeha ili koja je verovatnoća neuspeha? Koristeći verovatnoću i statističke podatke, možemo da predvidimo verovatnoću posmatranog događaja ili ishoda i na osnovu toga da donesemo odgovarajući zaključak i odluku koja je važna za našu kompaniju.

Osnovno pitanje je šta je tačno verovatnoća? Najjednostavnije, to je šansa da se nešto desi. Strogo govoreći, treba prvo definisati eksperiment i elementarne ishode, a zatim događaj. U zavisnosti od problema koji se razmatra, eksperiment može da bude bacanje kockice za igru, na primer jednom, i registruje se pali broj, ili baca se novčić koji ima na jednoj strani pismo, a na drugoj grb, i registruje se pala strana, ili trči se maraton i registruje se vreme njegovog istrčavanja. Događaj je jedan skup nekih elementarnih ishoda, povoljnih za odgovarajuće posmatranje. Sada možemo uvesti strogu definiciju verovatnoće, koja je sledeća.

Definicija: Verovatnoća je šansa da se neki događaj desi.

Naš cilj je da izračunamo verovatnoću događaja kako bismo utvrdili da li je on relativno verovatan ili nije. Tako je verovatnoća izražena u proncentima, ili razlomkom, ali je preferirani oblik realna vrednost između 0 i 1. Ako događaj ima verovatnoću 1 onda je to siguran događaj, ukoliko ima verovatnoću jednaku 0, to je nemoguć događaj. Dajemo dalje definiciju verovatnoće odgovarajućeg događaja.

Definicija: Ukoliko je A neki događaj, verovatnoća događaja A, u oznaci P(A), se računa na sledeći način:

Razmotrimo nekoliko primera.

Primer1. Ukoliko bacamo pravilan novčić jednom, kolika je verovatnoća da je palo pismo?

Odgovor: U ovom eksperimentu moguća su 2 ishoda, da padne pismo (P) ili da padne grb (G). Događaj koji nas zanima jeste da padne pismo, tako da je ukupno jedan povoljan ishod. Tražena verovatnoća je:

Primer2. Ukoliko bacamo pravilan novčić dva puta, kolika je verovatnoća da je grb pao dva puta?

Odgovor: U ovom eksperimentu moguća su 4 ishoda: da padne pismo 2 puta, da padne grb 2 puta, da padne pismo pa grb i da padne grb pa pismo, tj. PP, GG, PG i GP. Događaj koji nas zanima jeste da padne pismo 2 puta. To je jedan povoljan ishod od ukupno četiri ishoda, pa je tražena verovatnoća:

Napomena: Ovde bi mogli da istaknemo i drugi koristan način za izračunavanje tražene verovatnoće iz prethodnog zadatka, za čije je razumevanje potrebno poznavanje nezavisnosti događaja, što će biti detaljnije objašnjeno kasnije. Naime, ako su dva događaja A i B nezavisna, tada se verovatnoća da se dese istovremeno oba događaja računa kao proizvod verovatnoće da se desi događaj A i verovatnoće da se desi događaj B, tj.

gde AB označava da su se desili i događaj A i događaj B, odnosno označava presek ta dva događaja, što ćemo kasnije detaljnije razmatrati. Onda je:

Primer3. Ukoliko bacamo kockicu za igru koja ima 6 strana, kolika je verovatnoća da će pasti broj 3?

Odgovor: U ovom eksperimontu moguća su 6 ishoda, da padne 1, 2, 3, 4, 5 ili 6; dok je povoljan 1 ishod, da padne 3. Tako je:

Primer4. Ukoliko bacamo kockicu za igru koja ima 6 strana, kolika je verovatnoća da će pasti broj deljiv sa 3?